Find kth largest element in an array

Tags: algorithm ruby heap max-heap projects

The other day I stumble upon the question to find the k^th largest element in the array. At first glance, I thought the solution was trivial. But later I thought that there are multiple ways to achieve efficient solution

Heap is a useful data structure when root of the tree is important. Extracting an element from the heap is in logarithmic time. This could be used to find k^th element from the array since finding maximum or minimum in heap is constant time.

Problem Statement

Suppose, we have an array of arbitrary integer values. We need to find the k^th largest element in the array. A sample of the input file is given below

3
9, 4, 5, 2, 1, 23, 55, 88, 74

Here, the first line is the value of n and next line contains the array

Desired Output

The output should print the 3^rd element in the array i.e.

55

Step 1 aka Read the input file

Before we begin, we need to perpare our tools and gather required inputs. First we need to read the input file and get the value of k and the array. Also I'll be using ruby to write code as it is closer to psuedo code. So fire up your text editor and paste the code below

	filename = 'input.txt'
	#Read the file
	txt = File.open(filename, 'r')
	#get the first value
	n_value = txt.first
	#read the next line and split the line based on comma
	#and save it in array
	array_value = txt.first.split(',')
	txt.close

view raw nlargest_read_input.rb hosted with ❤ by GitHub

Step 2 aka the easy way

One of the first solution that pops in my mind to find the n^th largest element is

1. Sort the array in descending order
2. Get the element at the k^th index

The time complexity for this solution is @L O(n\log{}n) @L . However we can still find another solution in @L O(n) @L time.

More Efficiently?

We can visualize our array as tree with each value as a node of tree. However to build our array as heap , we need to satisfy certain properties

1. Each node of the heap has value
2. Value of each node @L \ge @L values of each of its children (Max-heap)

In a nutshell our array should look like this

88,74,23,55,1,5,9,2,4

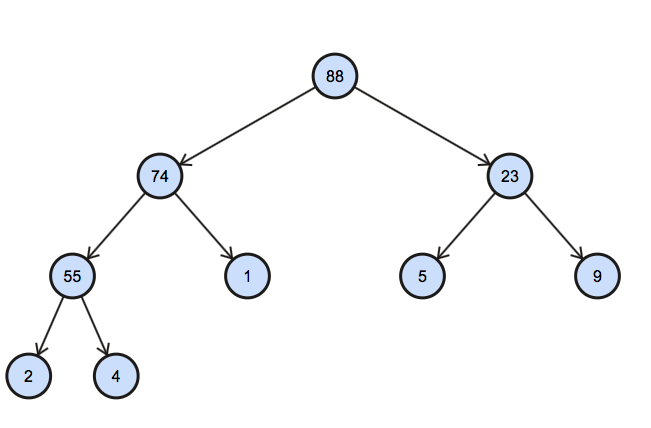
Building the heap

Building heap takes O(n) time. First visit to every non-leaf node and checks if the value at the node satisfy heap property.

	# build heap
	# time O(n) time
	def build_heap(nums)
	nums_size = nums.length
	# get all the non-leaf nodes
	i = (nums_size / 2) - 1
	while i >= 0
	#heapify it
	max_down(nums, i, nums.length)
	i = i - 1
	end
	end

view raw build_heap.rb hosted with ❤ by GitHub

Max_down() is the most important function as it heapifies (or maintain the heap property).

	# Maxheap
	def max_down(nums, i, nums_size)
	#debug = ''
	# check if the root element is greater than
	# left-most leaf
	if (2 * i + 1) < nums_size and nums[2 * i + 1] > nums[i]
	largest = 2 * i + 1
	else
	largest = i
	end
	# check if the largest element is greater than
	# rightmost leaf
	if (2*i +2) < nums_size and nums[2 * i + 2] > nums[largest]
	largest = 2 * i + 2
	end
	if defined? debug
	puts("i is " + i.to_s + " and A[i] is " + nums[i].to_s + " and largest is " + largest.to_s + " and A[largest] is " + nums[largest].to_s)
	end
	#if the root element needs to change
	# to statisfy the heap quality
	if i != largest
	#swap element
	swap_variable = nums[i]
	nums[i] = nums[largest]
	nums[largest] = swap_variable
	max_down(nums, largest, nums_size - 1)
	end
	end

view raw max_down.rb hosted with ❤ by GitHub

Extract Max

Our last step involves extracting the k^th max element.

1. Extract the fist element which is the root element @L O(1) @L
2. Call heapify to maintain heap property @L O(\log{}(n) @L
3. Call extract k times extract max @L O(k \log{}(n)) @L

	# get the leargest element
	# and heapify it
	# nums is the input array
	# nums_size is the length of the input array
	def extract_max(nums, nums_size)
	elem = nums[0]
	nums[0] = nums[nums_size - 1]
	# now the size reduces by 1
	# heapify it
	max_down(nums, 0, nums_size - 1)
	return elem
	end
	# nums is the input array
	# k is the k^th largest elment in array
	def k_largest(nums, k)
	#building a heap and inserting array's elements into heap
	build_heap(nums)
	#get the largest element
	nums_size = nums.length
	i = 0
	while i < k
	elem_max = extract_max(nums, nums_size)
	nums_size = nums_size - 1
	i = i + 1
	end
	return elem_max
	end

view raw max_extract.rb hosted with ❤ by GitHub

Conclusion

Time complexity analysis of two methods discussed above

Using	Worst Case	Description
Sort	O(n log(n)) + O(1)	Sorting the array + accessing the element
Heap	O(n) + O(k log(n))	Building heap + extracting maximum element

---