Quickly sort large file in linear time

Tags: lsd radix sort sorting cplusplus

Any deterministic general sorting algorithm has an average-case time complexity of Ω(nlogn). However, certain sorting algorithms can run faster in O(n) but with limitations¹. Instead of comparison-based sorting, each element is examined individually based on its value. Radix sort is a prime example of an integer sorting algorithm.

Problem Statement

Suppose, we have large directory containing names of people in random order. The names need not be distinct. We need to sort the name in the ascending order. Also our algorithm should run in linear time. A sample of the input file is shown below²

JAMES          1.664  1.664      1
TUSHARSHARMATUSHARSHARMA   1.99 3
JOHN           1.642  3.305      2
ROBERT         1.576  4.881      3
MICHAEL        1.321  6.202      4
MARY           1.319  7.521      5
WILLIAM        1.230  8.750      6
DAVID          1.185  9.934      7
RICHARD        0.854 10.788      8
CHARLES        0.765 11.552      9
JOSEPH         0.705 12.257     10
THOMAS         0.692 12.948     11
PATRICIA       0.539 13.486     12
CHRISTOPHER    0.519 14.005     13
LINDA          0.518 14.523     14
BARBARA        0.490 15.013     15

Desired Output

The output file contains the names read from the file and sort them alphabetically.

AARON
ABBEY
ABBIE
ABBY
ABDUL
ABE
ABEL
ABIGAIL
ABRAHAM
ABRAM
ADA
ADAH
ADALBERTO
ADALINE

NOTE: Each line is read upto k = 21 characters (arbitrary). Any character after 21st position is truncated.

Radix Sort

Radix sorts the integer by their least significant @L \mathtt{d}@L bits. @L \mathtt{w}/\mathtt{d}@L passes are made to counting-sort which sorts @L \mathtt{w}@L-bit integers. Following could be easily implemented in C++.

void lsdRadixSort(char S[][k])
{
 
    for (int d = k - 1; d >=0 ; d--) {
        countingSort(S, d);
    }
   
}

Procedure lsdRadixSort reads an array S of size n * k. For each d integers, it passes array and the index to countingSort procedure. The main sorting occurs at Counting Sort.

Counting Sort

Counting sort an array of integer of length n. Radix sort uses several passes of Counting Sort to sort the array of size n * k . The algorithm works like this

Count frequencies of each letter using key as index
Compute frequency cumulates
Access cumulates using key as index to find record positions.
Copy back into original array

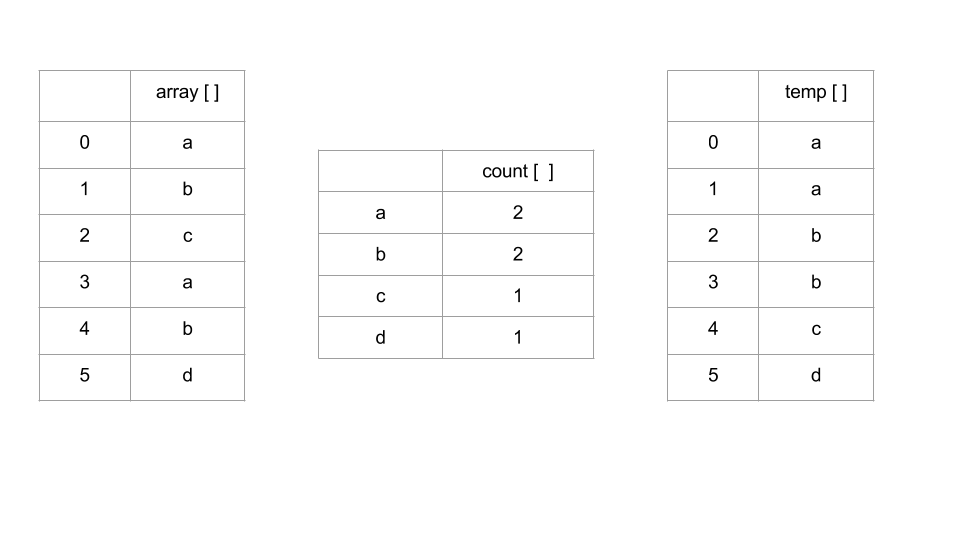
Following is the C++ implementation of Counting Sort.

void countingSortSwap(char S[][k], int j)
{
    //here j is the column 

    int count[256] = {0};

    char temp[n][k];
    temp[0][0] = ' ';


    for (int i = 0; i < n; i++) {
        int valueChar = (int) S[i][j];
        count[valueChar + 1]++;
    }

    for (int p = 1; p < 256; p++) {
        count[p] += count[p - 1];
    }

    for (int i = 0; i < n; i++) {
        int valueChar = (int)S[i][j];
        int index = count[valueChar++]++;
        for (int p = 0; p < k; p++) {
            temp[index][p] = S[i][p];
        }
    }

    for (int i = 0; i < n; i++) {
        for (int p = 0; p < k; p++) {
            S[i][p] = temp[i][p];
        }
    }


}

More Efficiently?

Radix sort can also be implemented without avoiding the hassle of moving the array to and fro. We use a pointer array (array of string indices) indexP[0..n−1]. Initially, set indexP[i] = i for all i. During the sorting, we move these indices. At the end of sorting, indexP[0] will be the index of the string which is the first in the sorted order, indexP[1] the second string in the sorted order, and so on.

We also declare prevIndex[0..n-1] to keep track of indicies of previous sorting. Thus our lsdRadixSort procedure would be slighlty different as

void lsdRadixSort(char S[][k], int indexP[])
{
    int count[k];
    int prevIndex[n];
 
   for (int d = 0; d < n ; d++ )
        prevIndex[d] = d;

    for (int d = k - 1; d >=0 ; d--) {
        countingSortp(S, d, indexP, prevIndex);
    }

}

Following is the new C++ implementation of Counting Sort.

void countingSort(char S[][k], int j, int indexP[], int prevIndex[])
{
    //here j is the column 

    int count[256] = {0};

    int tempCount[n];
    memset(tempCount, 0, sizeof(int) * n);

    for (int i = 0; i < n; i++) {
        int valueChar = (int) S[prevIndex[i]][j];
        count[valueChar + 1]++;
    }

    for (int p = 1; p < 256; p++) {
        count[p] += count[p - 1];
    }
 
    for (int i = 0; i < n; i++) {
        int valueChar = (int)S[prevIndex[i]][j];
        int index = count[valueChar++]++;

        tempCount[index] =   prevIndex[i];
    }

    for (int i = 0; i < n; i++) {
        indexP[i] = tempCount[i];
        prevIndex[i] = tempCount[i];
    }
}

Finally we print the names in ascending order in the file as per as the sorted indexP[0 .. n-1].

printToFile(char S[][k], string filename, int indexP[])         
{
    int tempP[n];
    memset(tempP, 0, sizeof(int) * n);

    fo.open\(filename.c\_str\(), ios::out | ios::binary);
    if (!fo) {
        cout<<"Error opening the file\n";
        exit(-1);
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < k; j++) {
            fo <<S[indexP[i]][j];
        }
        fo<<endl;
    }

}

Conclusion

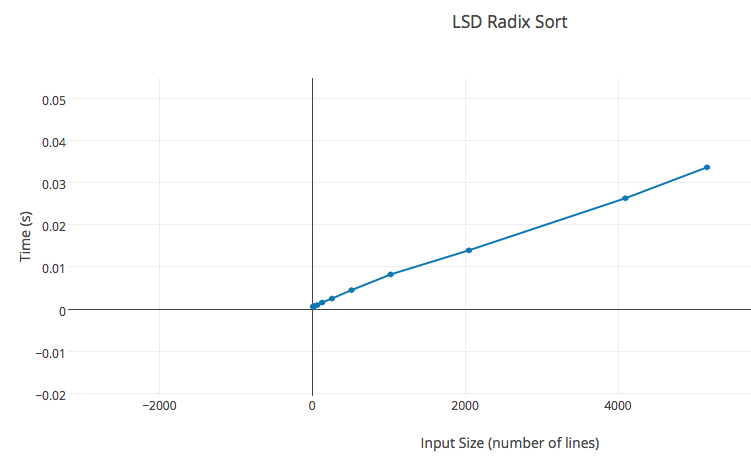
The sort runs in linear time as discussed earlier. Below is time it took against input of different size.

n	k	time (s)
8	21	0.000591
16	21	0.000674
32	21	0.000762
64	21	0.000961
128	21	0.001582
256	21	0.002517
512	21	0.004514
1024	21	0.008236
2048	21	0.013947
4096	21	0.0263
5164	21	0.033631

Download the code

Footnotes

Special case for Integers
↩
Assuming that the names are not greater than arbitrary number k
↩